8. E=mc^2 #2

8. 특수 상대성 이론의 결과5


E.2.    #2


앞에서 이 방정식이 질량 = 에너지 등가 방정식이 아닐 뿐만 아니라, 수식 자체도 틀렸다고 했습니다. 그렇다면 이 방정식의  바른 풀이는 어떻게 되는지 살펴 보도록 하겠습니다.


빛(전자기파)은 전자의 진동으로부터 발현 된다고 했습니다. 그렇다면 전자의 진동에 관해서 살펴봄으로써 빛의 근원적인 에너지량에 대해서 쉽게 알 수 있을 것입니다.


도선에서 전류의 속도가 빛의 속도와 같다는 것은 널리 알려진 사실입니다. 이것으로부터 전자의 평균속도가 30만km/s 라는 것을 알 수 있습니다. 전자의 평균속도가 30만km/s 라면, 전자의 최저속도와 최고속도 그리고 가속도는 얼마일까요?


전자의 진동이 전류의 흐름이기때문에 전류의 속도에서 전자의 평균속도와 최대속도 , 최저속도를 다음과 같은 수식으로 정의 되기 때문에   

전자의 최저속도 v0 = 0km/s , 최고속도 Vmax = 2 X Vag = 2c = 60만km/s 가 됩니다. 여기서 전자의 가속도를 구하면 가속도

가 됩니다. 이것은 전자 진동의 반주기 동안의 전자의 가속도 입니다. 이 가속도를 이용하여 전자의


 힘을 구하면 F= ma 에서  이 됨니다. 여기서 m은 전자의 질량이며 c는 빛의 속도, f는 빛의 주파수 (전자의 진동 주파수) 입니다.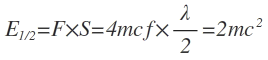


이 사실로 부터 전자 진동의 에너지를 구하면 , E = F X S , S는 진행한 거리 이기 때문에 전자진동의 반주기 동안의 이동거리는  이고, 파장은 이므로 전자 진동의 1/2주기 동안의 에너는
 이 됩니다. 따라서



전자가 1주기 움직이는데 소요되는 에너지는 이 됩니다.

 

빛(전자기파)은 전자 진동에 수직한 평면으로 방사되기 때문에. 거리에 따른 빛의 에너지량은  

여기 r은 전자의 진동으로부터 빛(전자기파)이 진행한 거리 입니다. 전자의 진동으로부터 빛의 진행에 따른 한 점에서의 빛 에너지가 Epint 와 같이 구해지기 때문에 빛의 발현으로부터 거리 r=0.6366m 떨어진 곳에서의 빛 에너지는 입니다.


19세기 과학자들이 연구한 결과값이 또는 이 것으로 측정 되었던 것은 빛의 발현 시점으로부터 거리가 조금씩 달랐기 때문입니다. 결론적으로 빛의 에너지 방정식은 이 아니라 , 이 것이 되어야 합니다.


죄송합니다. 온라인 글쓰기에 조금 어려움이 있네요. 자세한 내용은 저의 책 - 빛의 절대 좌표 이론 ( 아인슈타인의 상대성 이론은 틀렸다)에 자세한 내용이 있습니다.  책은 온라인 및 오프라인 서점에 있습니다.